Higher-order Graph Convolutional Network with Flower-Petals Laplacians on Simplicial Complexes
 HiGCN
HiGCNAbstract
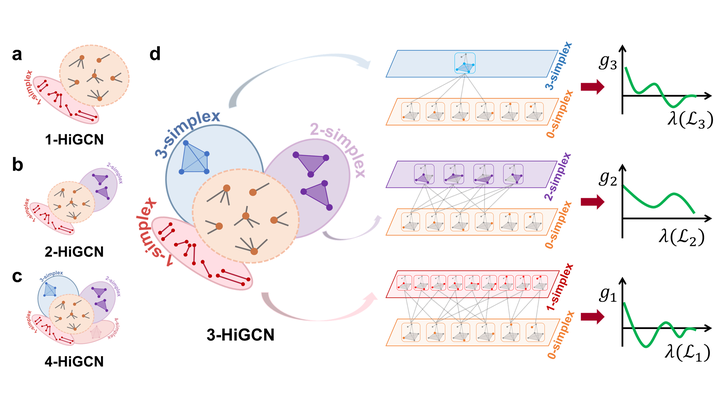
Despite the recent successes of vanilla Graph Neural Networks (GNNs) on many tasks, their foundation on pairwise interaction networks inherently limits their capacity to discern latent higher-order interactions in complex systems. To bridge this capability gap, we propose a novel approach exploiting the rich mathematical theory of simplicial complexes (SCs) - a robust tool for modeling higher-order interactions. Current SC-based GNNs are burdened by high complexity and rigidity, and quantifying higher-order interaction strengths remains challenging. Innovatively, we present a higher-order Flower-Petals (FP) model, incorporating FP Laplacians into SCs. Further, we introduce a Higher-order Graph Convolutional Network (HiGCN) grounded in FP Laplacians, capable of discerning intrinsic features across varying topological scales. By employing learnable graph filters, a parameter group within each FP Laplacian domain, we can identify diverse patterns where the filters’ weights serve as a quantifiable measure of higher-order interaction strengths. The theoretical underpinnings of HiGCN’s advanced expressiveness are rigorously demonstrated. Additionally, our empirical investigations reveal that the proposed model accomplishes state-of-the-art (SOTA) performance on a range of graph tasks and provides a scalable and flexible solution to explore higher-order interactions in graphs.
Supplementary notes can be added here, including code and math.